Уравнение состояния для Ае- и Аеп-фаз вещества

Мы будем иметь дело с моделями звездных конфигураций, состоящих из вырожденных газовых масс. Это конфигурации белых карликов и барионных звезд. Под последними подразумеваются модели небесных тел, состоящих из вырожденного барионного газа. В расчетах параметров этих звездных конфигураций нужно иметь уравнение состояния вещества. Нас интересуют только вырожденные состояния вещества.

Начнем с рассмотрения Ае-фазы. Она состоит из голых атомных ядер и свободного вырожденного электронного газа. При достаточно низких температурах движение ядер сводится лишь к тому, что они совершают нулевые колебания около фиксированных точек равновесия. Поэтому они не дают никакого вклада в давление вещества. Давление целиком обусловлено электронами, плотность же энергии определяется атомными ядрами.

Плотность энергии равна

ρ = (тпс2 +b)∑ 2 Акпк + e (1)

где b — средняя энергия связи нуклона в ядрах (здесь нет смысла различать массы протона и нейтрона), пк — число ядер данного типа (с параметрами Ак и Zк) в единице объема, ρе — плотность энергии электронного газа. В условиях наличия вырожденного электронного газа b является функцией е .Согласно

ρе = 4Ке(хе (1 + 2х2e)-(хе + )) (2)

где, хе = ρе/mес = (3)1 /3hne1/3 me с — граничный импульс электронов в единицах mес (при ре>> тес, хе = е/те с2) и

Ке (3)

Иногда удобно взамен хe использовать параметр tе:

tе =4arsh xe (4)

С помощью этого параметра плотность энергии электронов запишется в следующем компактном виде:

ρe = Ке(sh te- te). (5)

В выражении энергии (1) можно произвести некоторые упрощения. Так,

∑Aknk=∑Zknk=ne

где А/Z есть средняя величина отношения Ак/Zк (усредненная по всем типам ядер, имеющихся в среде). Учитывая последнее и пренебрегая малыми величинами b и ρе, получаем

ρ=(6)

Напомним, что из-за явления нейтронизации отношение А/ Z является функцией хе, эта зависимость аппроксимирована полиномом. Теперь вычислим давление. Оно равно производной энергии по объему с обратным знаком, при постоянном числе частиц и энтропии (в данном случае энтропия равна нулю). Так как парциальное давление ядер не учитывается, то

P=-(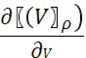)Ne=-()Ne

где Nе = Vпе — число электронов в некотором объеме V. При дифференцировании ρе нужно учесть, что хе зависит от объема V. Имея в виду (2), находим для давления

Интересные статьи:

Сварка в космосе
Введение В конце 50-х годов нашего столетия родилась новая отрасль человеческой деятельности — космонавтика. Об этом на весь мир возвестили сигналы первого советского спутника Земли, утвердив тем самым ведущую роль нашей страны в освоени ...

Созвездие Ориона
Введение В темную, безоблачную ночь на небе видно множество звезд и созвездий. Но на всем небе нет иного созвездия, которое бы содержало столько интересных и легко доступных для наблюдателя объектов, как Орион (Orion). Орион - одно из д ...

Обзор систем координат, использующихся в астрономических расчетах
Горизонтальная топоцентрическая система координат В этой системе центр помещается в месте нахождения наблюдателя на поверхности земли, основной плоскостью является плоскость математического горизонта. Одной координатой при этом является ...