ЭЛЕМЕНТЫ СФЕРИЧЕСКОЙ ТРИГОНОМЕТРИИ

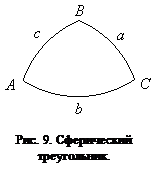Сферическим треугольником называется фигура на поверхности сферы, образованная пересечением трёх дуг больших кругов этой сферы (рис. 9). Вершины сферического треугольника принято обозначать большими буквами латинского алфавита, а противолежащие этим сторонам угла – соответственно малыми буквами.

Каждая сторона сферического треугольника меньше суммы двух других сторон:

.

Каждая сторона сферического треугольника больше разности двух других его сторон:

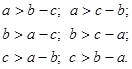
Полупериод сферического треугольника всегда больше каждой из его сторон:

Сумма сторон сферического треугольника всегда меньше 360°:

360°.

Сумма углов сферического треугольника всегда меньше 540° и больше 180°:

540°180°.

Разность между суммой трёх углов сферического треугольника и 180° называется сферическим избытком Е:

180°.

Площадь сферического треугольника s равна произведению сферического избытка на величину :

, (8)

где R – радиус сферы, на поверхности которой образован треугольник.

Косинус одной стороны сферического треугольника равен сумме произведения косинусов двух других его сторон и произведения синусов тех же сторон на косину угла между ними:

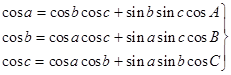. (9)

Синусы сторон сферического треугольника пропорциональны синусам противолежащих им углов:

. (10)

или

. (11)

Синус стороны сферического треугольника, умноженный на косинус прилежащего угла, равен произведению синуса другой стороны, ограничивающей прилежащий угол, на косинус третьей стороны минус косинус стороны, ограничивающей угол, умноженный на произведение синуса третьей стороны на косинус угла, противолежащего первой стороне:

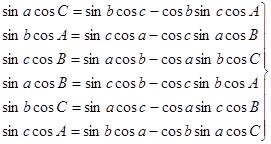. (12)

Полярным треугольником для данного сферического треугольника называется такой сферический треугольник, по отношению сторон которого вершины данного являются полюсами, то есть отстоят от сторон на 90° (рис. 10).

Сумма угла данного сферического треугольника и соответствующей стороны полярного треугольника равна 180°:

(13)

и наоборот:

. (14)

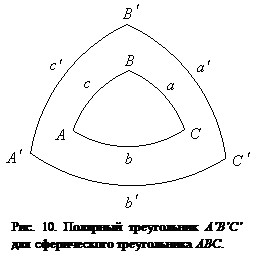На основе этих свойств полярного треугольника и исходя из (8) – (12), можно получить другие зависимости между сторонами и углами сферического треугольника. Так, например:

.

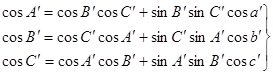Эти формулы, равно как и другие, которые могут быть получены на основании выражений (13) и (14), справедливы не только для полярного треугольника, но и вообще для всякого сферического треугольника.

Если в сферическом треугольнике один из углов равен 90°, то треугольник называется прямоугольным. Для решения прямоугольных сферических треугольников наиболее употребительны следующие формулы:

.

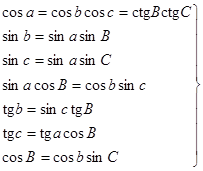Для решения сферических треугольников со стороной a = 90° употребляются следующие формулы:

.

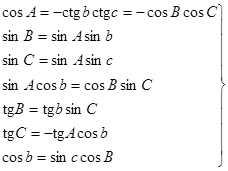Интересные статьи:

Исследование законов Вселенной
Вселенная, Пространство, время согласно выводам теоретического исследования свойств множества хаотически движущихся в Пространстве абсолютно упругих частиц разных величин. Невозможно не согласиться, что время – это последовательность соб ...

Венера
Венера - вторая после Меркурия по удаленности от Солнца (108млн.км) планета земной группы. Ее орбита имеет форму почти правильного круга (эксцентриситет 0,007). Венера совершает облет Солнца за 224,7 земных суток со скоростью 35 км/сек. ...

Уравнение состояния сверхплотного вещества
Уравнение состояния для Ае- и Аеп-фаз вещества Мы будем иметь дело с моделями звездных конфигураций, состоящих из вырожденных газовых масс. Это конфигурации белых карликов и барионных звезд. Под последними подразумеваются модели небесных ...