При этом взаимодействие между телами M1 и M2 не учитывается. Если рассмотреть движение планет вокруг Солнца, в этом случае , и , то получится формулировка третьего закона, данная самим Кеплером:

.

Третий закон Кеплера можно также выразить как зависимость между периодом T обращения по орбите тела с массой M и большой полуосью орбиты a (G – гравитационная постоянная):

.

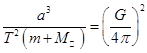Здесь необходимо сделать следующее замечание. Для простоты часто говорится, что одно тело обращается вокруг другого, но это справедливо только для случая, когда масса первого тела пренебрежимо мала по сравнению с массой второго (притягивающего центра). Если же массы сравнимы, то следует учитывать и влияние менее массивного тела на более массивное. В системе координат с началом в центре масс орбиты обоих тел будут коническими сечениями, лежащими в одной плоскости и с фокусами в центре масс, с одинаковым эксцентриситетом. Различие будет только в линейных размерах орбит (если тела разной массы). В любой момент времени центр масс будет лежать на прямой, соединяющей центры тел, а расстояния до центра масс r1 и r2 тел массой M1 и M2 соответственно связаны следующим соотношением:

.

Перицентры и апоцентры своих орбит (если движение финитно) тела также будут проходить одновременно.

Третий закон Кеплера можно использовать, чтобы определить массу двойных звезд.

Пример.

– Какова была бы большая полуось орбиты планеты, если бы синодический период ее обращения равнялся одному году?

Из уравнений синодического движения находим сидерический период обращения планеты. Возможны два случая:

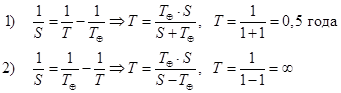
Второй случай не реализуется. Для определения «а» пользуемся 3 законом Кеплера.

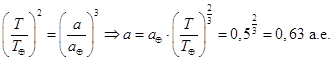
В солнечной системе такой планеты нет.

Эллипс определяется как геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов F1 и F2) есть величина постоянная и равная длине большой оси:

r1 + r2 = |AA/| = 2a.

Степень вытянутости эллипса характеризуется его эксцентриситетом е. Эксцентриситет

е = ОF/OA.

При совпадении фокусов с центром е = 0, и эллипс превращается в окружность.

Большая полуось a является средним расстоянием от фокуса (планеты от Солнца):

a = (AF1 + F1A/)/2.

Домашнее задание: § 6, 7. к. в.

1 уровень: 1 – 2 балла.

1. Укажите, какие из перечисленных ниже планет являются внутренними.

A. Венера. B. Меркурий. В. Марс.

2. Укажите, какие из перечисленных ниже планет являются внешними.

А.Земля. Б. Юпитер. В. Уран.

3. По каким орбитам движутся планеты вокруг Солнца? Укажите правильный ответ.

A. По окружностям. Б. По эллипсам. B. По параболам.

Интересные статьи:

Солнечные затмения
1. Картина полного солнечного затмения Полные солнечные затмения относятся к числу наиболее величественных и красивых явлений природы. В голубых просторах неба светит Солнце. Оно безраздельно господствует над земным шаром — над материка ...

Измерение времени
Измерение времени Ответить на вопрос «что такое время» нелегко. В самом общем виде можно сказать, что время – это непрерывная череда сменяющих друг друга явлений. Главное свойство времени состоит в том, что оно длится, течет безостановоч ...

Виды космических аппаратов
КОСМИЧЕСКИЕ АППАРАТЫ ИССЛЕДОВАНИЯ ПРИРОДНЫХ РЕСУРСОВ ЗЕМЛИ И КОНТРОЛЯ ОКРУЖАЮЩЕЙ СРЕДЫ СЕРИИ РЕСУРС-Ф Для исследования природных ресурсов Земли и контроля окружающей среды разработана космическая система Ресурс-Ф, которая включает в себя ...