По графикам и определяем характеристику прогрессивности горения заряда и коэффициент дегрессивно догорающих остатков .

.

Длина заряда

.

Угол раскрытия лучей

.

Радиус скругления .

Принимаем .

По таблице определяем значения углов

;

, из конструктивных соображений принимаем

Толщина свода заряда

.

Относительная длина заряда

.

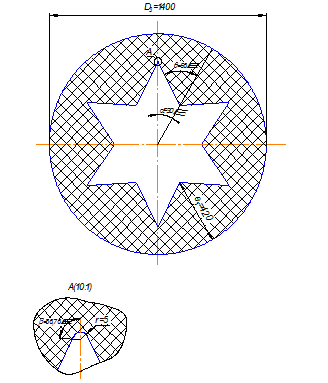
Рис.9. Звездообразный заряд со скругленными углами.

2.6 Расчет на прочность корпуса РДТТ

Расчет позволяет определить толщину элементов корпуса, находящихся под давлением газов в камере сгорания. Необходимо, чтобы корпус был прочным и имел минимальную массу и стоимость.

Исходные данные:

Давление в камере сгорания ;

Внутренний диаметр камеры ;

Материал обечайки камеры 28ХСНМВФА (СП-28);

Предел прочности ;

Модуль упругости .

Порядок расчета:

Толщина металлической обечайки корпуса

,

где коэффициент запаса прочности;

временное сопротивление материала обечайки с учетом нагрева.

.

коэффициент, учитывающий снижение прочности при нагреве (принимаем, что температура обечайки не превышает ), .

Интересные статьи:

Случайность в научной картине Вселенной
Научная мысль в процессе познания Вселенной всегда включала в себя идею случая. При этом исторически произошли весьма интересные изменения в самой постановке этой проблемы. В первоначальных представлениях о строении и эволюции мира, в перв ...

Проблемы изучения космоса
Сама проблема возникла еще в античности, когда философы задумывались над проблемами мироздания и системой движения планет. Однако глобальной эта проблема стала в середине XX века поле запуска первого спутника Земли 4.04.1957г. В данный мо ...

Открытие квазаров
Введение В истории астрономии, древнейшей из наук, не было времени, столь богатого самыми выдающимися открытиями, как наши дни. Особенно счастливыми оказались последние десятилетия, считая открытия квазаров в 1963 г. Было обнаружено рели ...