Третий закон Кеплера (Гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.

,

где T1 и T2 — периоды обращения двух планет вокруг Солнца, а a1 и a2 — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:

,

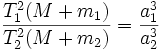где M – масса Солнца, а m1 и m2 – массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Шестью элементами, определяющими гелиоцентрическую невозмущённую О. н. т. Р (рис.), являются:

наклон орбиты к плоскости эклиптики i.

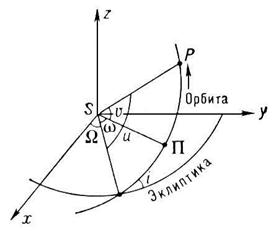
Может иметь любое значение от 0 до 180°; наклон считается меньшим 90°, если для наблюдателя, находящегося в северном полюсе эклиптики, движение планеты имеет прямое направление (против часовой стрелки), и большим 90° при обратном движении. Долгота узла W. Это — гелиоцентрическая долгота точки, в которой планета пересекает эклиптику, переходя из Южного полушария в Северное (восходящий узел орбиты). Долгота узла может принимать значения от 0 до 360°.Большая полуось орбиты а. Иногда вместо а в качестве элемента орбиты принимается среднее суточное движение n (дуга орбиты, проходимая телом за сутки). Эксцентриситет орбиты е. Если b – малая полуось орбиты, то е = /a. Вместо эксцентриситета иногда принимают угол эксцентриситета j, который определяется соотношением sin j = е. Расстояние перигелия от узла (или аргумента перигелия) w. Это гелиоцентрический угол между восходящим узлом орбиты и направлением на перигелий орбиты, измеряемый в плоскости орбиты в направлении движения планеты; может иметь любые значения от 0 до 360°. Вместо элемента w применяется также долгота перигелия p = W + w. Элемент времени, т. е. эпоха (дата), в которую планета находится в определённой точке орбиты. В качестве такого элемента может служить, например, момент t, в который планета проходит перигелий. Положение планеты на орбите определяется аргументом широты и, который представляет собой угловое расстояние планеты вдоль орбиты от восходящего узла, или истинной аномалией v —угловым расстоянием планеты от перигелия. Аргумент широты меняется от 0 до 360° в направлении движения планеты. Аналогичными элементами определяются орбиты комет, Луны, спутников планет, компонентов двойных звёзд, Солнца в Галактике и др. небесных тел.

МЕТОДЫ КОСМИЧЕСКОЙ ГЕОДЕЗИИ

Интересные статьи:

Жизнь на Марсе
ВВЕДЕНИЕ Полёт к Марсу – трудное дело. Это не к бабушке в гости съездить. Мы сделали всё, что могли. Единственное, что мы не можем сделать – предотвратить невезение. Эдвард Вейлер, руководитель Управления космической науки NASA Планета М ...

Проявление солнечной активности в геофизических параметрах
ВВЕДЕНИЕ Проблема «Солнце – Земля» является на сегодняшний день актуальной по многим причинам. Во-первых, это проблема альтернативных источников энергии на Земле. Солнечная энергия – неисчерпаемый источник энергии, притом безопасный. Во-в ...

Задачи астрономов во время наблюдений солнечных затмений (от 20-х годов ХХ века до наших дней)
Вступление Наблюдения затмившегося Солнца представляют исключительное научное значение. Весьма многочисленны те научные вопросы, для разрешения которых астрономы организуют экспедиции в полосу полных солнечных затмений, отправляясь подч ...