Основные понятия космической геодезии и астрономии

Страница 10

Это дифференциальное уравнение имеет общее решение:

u = \frac{GM}{\ell^2} \left[ 1 + e\cos(\theta-\theta_0) \right] .

для произвольных констант интегрирования e и θ0.

Заменяя u на 1/r и полагая θ0 = 0, получим:

r = { 1 \over u } = \frac{ \ell^2 / GM }{ 1+ e\cos\theta}.

Мы получили уравнение конического сечения с эксцентриситетом e и началом системы координат в одном из фокусов. Таким образом, первый закон Кеплера прямо следует из закона всемирного тяготения Ньютона и второго закона Ньютона.

Второй закон Кеплера (Закон площадей)

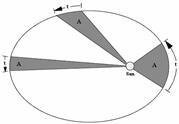
Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные времена радиус-вектор, соединяющий Солнце и планету, заметает сектора равной площади.

Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кепплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии бо́льшую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

По определению угловой момент \mathbf{L}точечной частицы с массой m и скоростью \mathbf{v}записывается в виде:

\mathbf{L} \ \stackrel{\mathrm{def}}{=}\ \mathbf{r} \times \mathbf{p} = \mathbf{r} \times ( m \mathbf{v} ).

где \mathbf{r}- радиус-вектор частицы а \mathbf{p} = m \mathbf{v} - импульс частицы.

По определению

\mathbf{v} = \frac{d\mathbf{r}}{dt} .

В результате мы имеем

\mathbf{L} = \mathbf{r} \times m\frac{d\mathbf{r}}{dt}.

Продифференцируем обе части уравнения по времени

\frac{d\mathbf{L}}{dt} = (\mathbf{r} \times \mathbf{F}) + \left( \frac{d\mathbf{r}}{dt} \times m\frac{d\mathbf{r}}{dt} \right)= ( \mathbf{r} \times \mathbf{F} ) + ( \mathbf{v} \times \mathbf{p} ) = 0

поскольку векторное произведение параллельных векторов равно нулю. Заметим, что F всегда параллелен r, поскольку сила радиальная, и p всегда параллелен v по определению. Таким образом можно утверждать, что |\mathbf{L}|- константа.

Страницы: 5 6 7 8 9 10 11 12 13 14

Интересные статьи:

Двойные звёзды
Двойные звезды Двойные звезды — это две (иногда встречается три и более) звезды, обращающиеся вокруг общего центра тяжести (см. Рисунок). Существуют разные двойные звезды: бывают две похожие звезды в паре, а бывают разные (как правило, э ...

Фотографические наблюдения метеорных потоков
Введение Ясной тёмной ночью, наблюдая величественную и неповторимую по своей красоте панораму неба, усеянную тысячами звезд и серебряный пояс Млечного Пути, можно заметить, как вдруг бесшумно быстро прочерчивает небо яркая «падающая звез ...

Строение Солнечной системы
Возникновение Солнечной системы Космогония- это научная дисциплина, раздел астрономии, в котором изучается происхождение и развитие небесных объектов- галактик, звезд и планет. Звездная космогония исследует процесс возникновения и жизне ...