Основные понятия космической геодезии и астрономии

Страница 9

\mathbf{a} = \frac{d^2\mathbf{r}}{dt^2} = f(r)\hat{\mathbf{r}}.

Вспомним, что в полярных координатах

\frac{d\mathbf{r}}{dt} =\dot r\hat{\mathbf{r}} + r\dot\theta\hat{\boldsymbol\theta},

\frac{d^2\mathbf{r}}{dt^2} = (\ddot r - r\dot\theta^2)\hat{\mathbf{r}} + (r\ddot\theta + 2\dot r \dot\theta)\hat{\boldsymbol\theta}.

В координатной форме запишем

\ddot r - r\dot\theta^2 = f(r),

r\ddot\theta + 2\dot r\dot\theta = 0.

Подставляя \ddot \thetaи \dot rво второе уравнение, получим

r { d \dot\theta \over dt } + 2 {dr \over dt} \dot\theta = 0,

которое упрощается

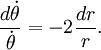
\frac{d\dot\theta}{\dot\theta} = -2\frac{dr}{r}.

После интегрирования запишем выражение

\log\dot\theta = -2\log r + \log\ell,

\log\ell = \log r^2 + \log\dot\theta,

\ell = r^2\dot\theta,

для некоторой константы \ell, которая является удельным угловым моментом (\ell=\mathbf{r}\times \mathbf{v}).Пусть

r = \frac{1}{u},

\dot r = -\frac{1}{u^2}\dot u = -\frac{1}{u^2}\frac{d\theta}{dt}\frac{du}{d\theta}= -\ell\frac{du}{d\theta},

\ddot r = -\ell\frac{d}{dt}\frac{du}{d\theta} = -\ell\dot\theta\frac{d^2u}{d\theta^2}= -\ell^2u^2\frac{d^2u}{d\theta^2}.

Уравнение движения в направлении \hat{\mathbf{r}}становится равным

\frac{d^2u}{d\theta^2} + u = - \frac{1}{\ell^2u^2}f\left(\frac{1}{u}\right).

Закон всемирного тяготения Ньютона связывает силу на единицу массы с расстоянием как

f \left( {1 \over u} \right) = f(r)= - \, { GM \over r^2 } = - GM u^2

где G — универсальная гравитационная константа и M — масса звезды.

В результате

\frac{d^2u}{d\theta^2} + u = \frac{GM}{\ell^2}.

Страницы: 4 5 6 7 8 9 10 11 12 13 14

Интересные статьи:

Жизнь на Марсе
ВВЕДЕНИЕ Полёт к Марсу – трудное дело. Это не к бабушке в гости съездить. Мы сделали всё, что могли. Единственное, что мы не можем сделать – предотвратить невезение. Эдвард Вейлер, руководитель Управления космической науки NASA Планета М ...

Основные сведения о Венере
Введение Древние греки дали этой планете имя своей лучшей богини Афродиты, римляне же потом переиначили по-своему и назвали планету Венерой, что, в общем, одно и то же. Однако случилось это не сразу. Одно время считалось, что в небе наход ...

Зарождение Солнечной системы
Формирование Солнечной системы В примечании к своему знаменитому трактату "Математические начала натуральной философии" Ньютон пишет: "… удивительное размещение Солнца, планет и комет может быть только творением всемогущег ...