которое будет встречаться в дальнейшем.

Рассмотрим два важных предельных случая уравнения состояния (8). В нерелятивистском случае параметр хе мал по сравнению с единицей. Разложим Р в ряд по степеням хе и отбросим малые величины в выражениях ρ и Р; исключая параметр х, получим

Р=Aρ5/3, (10)

Где

A= )5/3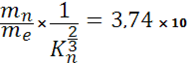-23 )5/3

Величина η= A/Z для всех ядер, за исключением водорода.

Р=B ρ4/3, (11)

Где

B=5,6410-14 )4/3

В выражении для плотности энергии мы опустили b и ρе.

Энергия связи нуклона в ядре имеет значение в интервале 0<b8 Мэв. У порога исчезновения Aе-фазы Р 1029 эргсм-3, а отношение парциальных плотностей энергии электронов и ядер порядка

Таким образом, b и ρе действительно достаточно малы и в расчетах звездных конфигураций не могут играть сколько-нибудь заметную роль.

В приведенном уравнении состояния не учтено взаимодействие частиц. Здесь мы имеем дело только с кулоновскими силами . Было показано, что потенциальная энергия электрона, обусловленная электрическими силами, мала по сравнению с его кинетической энергией, причем с возрастанием плотности отношение их уменьшается. Таким образом, приближение идеального газа здесь вполне оправдано. Ряд поправок к выражению давления (8), обусловленных кулоновскими взаимодействиями. Поправки к Р некоторую роль могут играть лишь при больших Z и х<1. Изменения, обусловленные температурой, тоже несущественны. Здесь важным является эффект зависимости А/Z от граничной энергии электронов.

Уравнение состояния (8) применимо до x=46, чему соответствует плотность ρ2,41032 эргсм-3. При больших плотностях мы имеем дело с Aen-фазой, где уравнение состояния другое.

Введем параметр

tn =4arsh xn ,

тогда ρп и Рп запишутся в следующем виде:

ρn=Kn(sh tn - tn),

Pn=Kn(sh tn - 8sh).(13)

Учитывая также энергию атомных ядер, парциальное давление и плотность энергии электронов, для уравнения состояния Aen-фазы вещества получаем

ρ=Kn(sh tn - tn)+mnc2,

P=Kn(sh tn - 8sh)+Pe.(14)

Здесь ρе и Рe —плотность энергии и давление электронного газа. Заметим, что чуть выше порога появления Aen-фазы парциальная плотность энергии и давление электронов (можно даже сказать — плотность энергии атомных ядер) достаточно малы по сравнению с соответствующими величинами для нейтронного газа. Здесь почти на всем протяжении фазы энергия и давление системы в основном определяются нейтронным газом.

Вообще говоря, в Aen-фазе следовало бы учитывать ядерные взаимодействия между нейтронами. Их вклад несуществен для энергии, но, по-видимому, является важным для давления: при заданном числе нейтронов учет ядерных сил приведет к уменьшению давления. Насколько нам известно, в рассматриваемой области плотностей теория ядерной материи как следует не разработана, поэтому мы довольствуемся приближением идеального газа. Уравнение состояния (14) справедливо в области плотностей 2,41032 ρ 5.451034 эргсм-3.

Об асимптотическом виде уравнения состояния

Целесообразно сначала исследовать асимптотическое поведение вида уравнения состояния при чрезвычайно больших плотностях. Здесь можно достичь определенного результата, исходя из совершенно общих соображений. В опытах по рассеянию быстрых протонов на нуклонах было установлено наличие весьма интенсивных сил отталкивания, действующих на расстояниях r210-14 см. Этот экспериментальный факт дает некоторое основание утверждать, что в надъядерной области с возрастанием плотности массы состояние барионной плазмы (мы говорим о барионной плазме, поскольку концентрация лептонов в ней очень мала) все больше отходит от газа и постепенно приближается к состоянию идеальной жидкости.

Интересные статьи:

Меркурий - горячая планета
Меркурий — первая от Солнца, самая внутренняя и наименьшая планета Солнечной системы, обращающаяся вокруг Солнца за 88 дней. Видимая звёздная величина Меркурия колеблется от −2,0 до 5,5, его нелегко заметить по причине очень малень ...

Жизнь на Марсе
ВВЕДЕНИЕ Полёт к Марсу – трудное дело. Это не к бабушке в гости съездить. Мы сделали всё, что могли. Единственное, что мы не можем сделать – предотвратить невезение. Эдвард Вейлер, руководитель Управления космической науки NASA Планета М ...

Система небесных координат
Системы небесных координатиспользуются в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Небесные координаты вводятся на геометрически правильной поверхности небесной сферы координатной сеткой, п ...